インドの子供は、日本の子供が九九を習うように、19の段までの2つの数の掛け算を暗記するといいます。
日本で教育を受けた、ましていい歳になってから19×19まで丸暗記するのは骨ですが、これくらいまでパッと答えが出ると、宴会の会費総額暗算するときに便利といえば便利そうです。
そんなわけで19の段までの掛け算の簡単な計算方法を考えてみました。
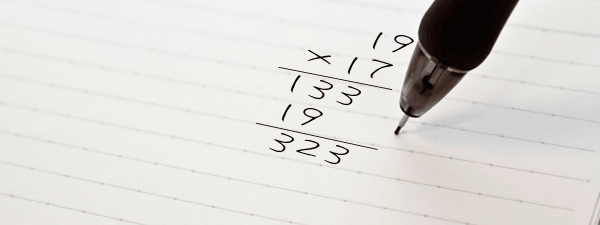
特に奇をてらった方法ではないんですが
というわけで、計算対象は1×1、1×2…19×18、19×19までの361通りの計算です。といっても9×9までの一桁同士の計算はみなさん暗記しているからそこは割愛。
ここではかける数、かけられる数のいずれか、または両方が19以下の2桁の数字の場合について考えます。
かける数、かけられる数がいずれも19以下の2桁の数の場合
m,nの2つの数が0以上9以下の1桁の整数であるとします。
19以下の2桁の2数とはつまり(10+m)、(10+n)と表すことが出来ます。
【例】19と17なら 19 = 10+9、17 = 10+7 よってm = 9、n = 7
19以下の2桁の整数の掛け算は(10+m)×(10+n)と表すことができますね?中学校の頃の数学を思い出していただくとわかりますが、これを展開してみると10×10+10×n+10×m+m×nとなります。
【例】19×17 = (10+9)×(10+7) = 10×10+10×7+10×9+9×7
もうお分かりかと思いますが、展開後の第1項は必ず100になります。2項目、3項目はm,nの10倍、つまりmとnの後にそれぞれ0(ゼロ)をつけただけ、4項目は…ただの1桁の九九の結果です。
【例】19×17 = 100+70+90+63 = 323
いや、まだ4数の足し算のプロセスがちょっと面倒そうです。なのでこのプロセスをもうちょっとわかりやすい順序に組み立てなおすとこんな感じになります。
19以下の2桁の2数 (10+m)、(10+n)【例として19と17、m=9、n=7】が与えられたとき、その掛け算は
- 一の位同士をかける。単純な九九【9×7 = 63】
- その結果の十の位にmを足す【153】
- さらにその結果の十の位にnを足す【223】
- 最後に百の位に1を足す【323】
どうでしょう、これなら計算プロセスごとの結果を3つ以上頭の中に覚えていなくても暗算で順次足していくだけなのでわりと簡単に計算結果を導けるんじゃないでしょうか。
かける数、かけられる数がいずれか一方が19以下の2桁の数、他方が1桁の数の場合
こちらは敢えて説明するほどのものでもないですけど…このパターンははるかに単純です。
1桁の数のほうをm、2桁の数のほうを(10+n)としましょう。
【例】7と14なら 14 = 10+4 よってm = 7、n = 4
2桁同士の場合と同じようにこの掛け算 m×(10+n) を展開すると 10×m+m×n となります。
【例】7×14 = 70+28 = 98
2桁同士の掛け算の場合と同様に組み立てなおすならば
- 一の位同士をかける。単純な九九【7×4 = 28】
- その結果の十の位にmを足す【98】
書いてわかりましたが、やっぱり説明するほどのことじゃありませんでしたね(笑)スミマセン。
オマケ・任意の2桁同士の掛け算は簡単にできるか?
ではさらに20以上99以下の数同士の掛け算が簡単にできるかどうか、ということなんですが。
任意の2桁の2数(10×a+m)、(10×b+n)の掛け算を展開すると
(10×a+m)×(10×b+n) = 100×a×b+10×a×n+10×b×m+m×n
となりましてなんだかちょっと面倒。
a×bとm×nは常に2桁以下の結果になり、a×bは100という係数がかかっているので、m×nとは2桁ずれる。つまり第1項と第4項の和は「十の位同士の九九の結果と1の位同士の九九の結果を左から順に並べる(ただし0は詰めない)」と表現できます。
また、第2項と第3項の和は「元の2数の互いの十の位と一の位をかけたものの和の十倍」と表現できそうです。
これを足し合わせれば元の計算結果がわかるわけですが…頭の中に一時的に記憶しておく数が多いのでいちいちメモしなきゃダメ?それなら普通に筆算したほうが早そうですよね。
なんだか世間では「東大生が開発した2桁同士の暗算術云々…」とか言うのが一時的に話題になったみたいなんですが、基本の計算方法は上に書いたことと同じようなので、あんまり効率化されてる気がしない気もしますw
そんなわけで、任意の2桁同士の掛け算はちょっと(ライフハック的な意味で)簡単に暗算は出来なさそうです。アカデミックな方法じゃなくてもう少し頭の中で創造しやすいグラフィカルな方法のほうがピンと来るかもしれません。もう少し検討してみて面白い方法思いついたらまた別のエントリで報告したいと思います。では。
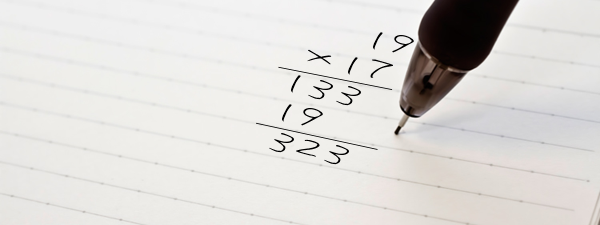


コメント