金属材料の強さはこうやって考えるのょ

370記事ほどこのブログで書いてるのに「そういや自分のフィールドの記事全く書いたことないなぁ」とふと思いたって、金属関係の材料力学とか設計とかその絡みの記事を書いてみることにしました。いやまぁリーマン生活はしのぎなんですけどね。どうも、私があの私です。

金属加工の便覧的なサイトはすでにたくさんあるんだけど、初学者向けのものすごい簡単な説明とか畑違いの人に興味持ってもらえるようなのはなかなかないなぁと思い。

追求すると深い世界なのでかなり端折って工学的にはウソくさい解説も書きますが直感的なわかりやすさ優先ということで。

「材料の強さを検証する」ということ
「応力」という考え方
引張られる金属棒の性質
変形と破壊
まとめ

「材料の強さを検証する」ということ

で、出だしで何を説明したらとっつきやすいかなと考えたんですが、まずは「材料の強さ」ってのがなんなのかってとこから始めたいと思います。

いきなり「材料の強さ」とか言われても知らん人にっては「ハァ？」って感じだと思いますが、機械や鋼構造物の、いわゆる設計作業の半分くらいは「作ったものが壊れないことの検証作業」だと言っていいと思います（残り半分は「機能」の検証、あと一部「意匠」が設計に含まれる場合もある）。

「材料の強さを検証する」ってのは大雑把に「変形のし難さ」と「破壊に対する保障」を考えることです。「変形と破壊は同じじゃん！」と思うかもしれませんが、実務上は別のものとして扱います。その違いを説明する前に以下のような例を見てみましょう。

「応力」という考え方

ここに一本の太さ一定の丸い鋼（鋼とは鉄（Fe）に純鉄だけでは得られない性質を鉄に付与するために材料に炭素やその他の元素[これを「合金元素」と言う]を混ぜたもの）の棒があります。

上図の矢印のように、棒鋼の両端を持って引張ってみましょう。棒鋼の両端を同じ強さの力で引張っているので、棒鋼内部を伝わって加えられた力がバランスしています。

引張る方向に直角な棒鋼の任意の断面（この場合は円形ですね、図のピンク色の部分）に注目してみるともちろんこの面についても力はバランスしています。

この様にある材料内部の仮想の面に働く面積辺りの力の大きさを「応力」と言います。応力σは力 F を断面積 A で割った値です。

左右に引張る力を F[N](Nは「ニュートン」、力の単位)、棒の直径を [mm]とすると、この棒の断面積 A は A = (πD^2)/4[mm^2]ですので、応力 σ は σ = F/A = 4F/(πD^2)[N/mm^2]と計算することが出来ます。あ、πは円周率です…ってのは説明しなくてもいいですよね？

この場合は棒の長さ方向に引張力を作用させているので特に「引張応力」と呼んだりします。

矢印の向きを変えると棒には圧縮力がかかるのでこの場合は「圧縮応力」と呼びますが、力の作用方向が逆のためFが負の値になるというだけで応力の本質は基本的に変わりません。

材料の破壊に対する強さを検証するときにはこの「応力」の値を持って評価することがほとんどですので「あぁそういうものなんだな」程度に覚えておきましょう。

引張られる金属棒の性質

さてこのように両端を持って引張ってみた棒鋼。実は引張るとその力に応じた分だけ長さが伸びてるんです。ま、直径1,2mmくらいの鋼棒でも人間の力で引張ったくらいではその変化は小さいので目で見てもわかりませんけどね。

引張るのをやめるとどうなるでしょうか。棒は元の長さに戻ります。この、力を加えると伸び力を取り除くと元に戻る性質を「弾性」と呼びます。

じゃぁどんどん強い力で引張れば棒は無限に伸びて、引張るのをやめると元に戻るか…というと、もちろんそんなことはありませんよね。金属材料が弾性を示すのはある限られた応力の範囲の中でのみです。お、ここで先ほどの応力が出てきましたね。

「引張荷重試験機」という機械があります。材料に引張力を加えたときに材料がどのような挙動を示すかを調べる機械です。

この引張荷重試験機で鋼材に加えた力と変形量との関係を調べると、以下のグラフのような挙動を示します。

ちなみに変形量は「ひずみ」といって、元の長さに対してどれくらいの長さが伸びたかという割合で表現します。

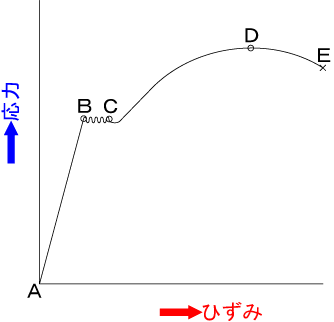
縦軸が応力、横軸がひずみです。

先ほど言った弾性を示す範囲はこのグラフで言うとＡ～Ｂの間だけです。この間の力ならば、それを取り除くとひずみは0になり長さは元に戻ります。グラフが直線なのでわかると思いますが、この間応力とひずみの関係は比例します。

Ｂ～Ｃは応力（加えている力）が一定なのに徐々に材料が伸びるというちょっと不思議な挙動を示す区間です。これを「材料の降伏」といいます。

またＢは「降伏点」といい、このときの応力を「降伏応力」と言います。

Ｃ～Ｄではまた応力が増えるとひずみが増える区間ですが、Ａ～Ｂ間とは違い曲線であり、応力とひずみは直線的な比例関係とはなりません。

Ｄ点で応力は最大となりその後は力を弱めても材料は伸び続けます。そしてＥ点に至って材料はついに千切れ（「破断」といいます）てしまいます。

さて、弾性の限度を超え（Ｂ点以降）たあとに力を加えるのをやめてしまうと材料はどうなるでしょう？

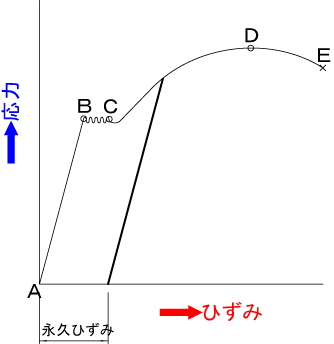
降伏応力を超える力を加えたあとにそれをやめても、ひずみの戻り方は最初の直線部分と平行に戻ろうとするので、力が０になっても永久ひずみが残ってしまうんですね。

余談ですが、鋼構造物に一般的に使われている軟鋼（SS400などの鋼種）は上図のようにハッキリとした降伏点が現れますが、ステンレス鋼（SUS304などの鋼種）のように弾性限とそのあとの最大応力までのカーブに明瞭な降伏点が現れないものもあり、弾性限度をどこにすればよいか困ってしまうことがあります。

そういった材質は0.1％（元の材料の長さの1/1000）の永久ひずみが発生する荷重を「0.1%耐力」と称し、降伏応力の代わりに設計時の基準応力として用いたりします。

変形と破壊

ということで、金属材料は力の加え加減で変形が元に戻る性質、力を解除しても戻らない永久ひずみ、そして破壊（破断）という何通りかのパターンがあるのがお分かりいただけたかと思います。

これらをどう使い分けるかと言う話ですが、例えば橋梁の桁などは常時は自動車の通行荷重などが作用しますが、これくらいで永久ひずみが出てしまうようでは橋の形が変わってしまうのでこれではいけません。かならず弾性限内で使用します。

一方で地震など非常時の力が作用する場合は多少変形しても破断に至って落橋しなければよしと考え常時より許容する力を軽減したりします。建築は私の専門外ですがおそらく似たような感じでしょう。

ベルトコンベヤなどの機械フレーム、ギヤボックスのケーシングなどは基本的に弾性限度内の荷重を想定して設計するのが普通です。かつその変形量もかなり小さくなるように設計します。フレームが変形することで歯車の噛み合わせやチェーンスプロケットの心間距離が変わってしまうようではそもそもその機能に支障をきたしてしまうからです。

コンピュータ関連製品のフレームなどは逆にその形を維持するギリギリの材料の強さしか考慮しないでしょう。量販品は材料コストを下げ保障の範囲を明確にした販売方法で価格を下げたほうがエンドユーザーにはありがたいですから。2階の窓からポータブルハードディスクを落として「壊れたじゃないか！」とわめく人は普通いないでしょう。

風呂の湯抜き栓についてるチェーン、あれは人間がちょっと強めに手で引張っただけで簡単に千切れます。もともとそういう使い方をするものではないからです。流れたりどこか別の場所においといて紛失しないためのものですから力のことなど考えずに極力安く作るのです。

このように「どこまでの変形・破壊を許容するか」はその製品の目的によって全然違います。強さとコストは通常トレードオフなのでその線引きをうまく見極めるのが設計者にとっては大事だと言うことですね。