業務用の計算処理(ちょっとした構造物の設計&計算書出力)のためスクリプト組んでるごろどくです。わからないこと調べ調べやってるんで進みが大変悪くて辛いです。CANVASとかいよいよ分らん…今回はCANVASの話ではないですけど。
JavaScriptにおける数値の丸めのことについて調べたらちょっとしたクセがあるようなのでまとめてみました。ご存知の方も復習を兼ねて読んでいただければと思います。
いきなりですがテストコード
解説の前にテスト用サンプルコードです。実際に動かしてもらった方が分かり良いと思います。それぞれのメソッドの返り値については各項目でキャプチャも入れておきますのでそちらも参考にしてください。
var x = [-1.51, - 1.50, - 1.49, 1.49, 1.50, 1.51];
var x_round = [];
var x_ceil = [];
var x_floor = [];
var x_trunc = [];
var x_parseint = [];
var x_tofixed = [];
var x_toprecision = [];
var x_toexponential = [];
for (var i = 0; i < 6; i++) {
x_round[i] = Math.round(x[i]);
x_ceil[i] = Math.ceil(x[i]);
x_floor[i] = Math.floor(x[i]);
x_trunc[i] = Math.trunc(x[i]);
x_parseint[i] = parseInt(x[i]);
x_tofixed[i] = x[i].toFixed(0);
x_toprecision[i] = x[i].toPrecision(1);
x_toexponential[i] = x[i].toExponential(0);
}
//alert("Math.round(num) ではn" + x + "nがn" + x_round + "nになります。");
//alert("Math.ceil(num) ではn" + x + "nがn" + x_ceil + "nになります。");
//alert("Math.floor(num) ではn" + x + "nがn" + x_floor + "nになります。");
//alert("Math.trunc(num) ではn" + x + "nがn" + x_trunc + "nになります。");
//alert("parseInt(num) ではn" + x + "nがn" + x_parseint + "nになります。");
//alert("num.toFixed(0) ではn" + x + "nがn" + x_tofixed + "nになります。");
//alert("num.toPrecision(1) ではn" + x + "nがn" + x_toprecision + "nになります。");
//alert("num.toExponential(0) ではn" + x + "nがn" + x_toexponential + "nになります。");
なぜ-1.51, – 1.50, – 1.49, 1.49, 1.50, 1.51なのか?正負の両方の場合の結果が確認できて、かつ「上の整数に近い数、下の整数に近い数、前後の整数のちょうど真ん中」なので。こうしておくと挙動を把握しやすいと思います。アラートのコメントアウト一個ずつ外してそれぞれ確認してみましょう。面倒くさい方用にサンプルページも置いておきますが、全部コメントアウト外してるので全部表示します。申し訳ない。
Mathオブジェクト
Mathオブジェクトには数値の丸めに関するメソッドとしてround()、ceil()、floor()そしてtrunc()の4つがあります。それぞれの丸めの処理は次のようになります。
round()メソッド
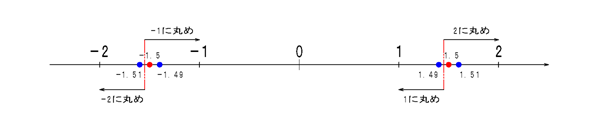
Math.round(num)は「引数として与えられた数値に最も近い整数を返す」メソッドです。最も近い整数が2つある、つまり小数点以下の端数が0.5ちょうどだった場合には+∞側の整数を返します。
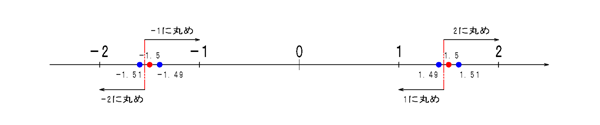
冒頭のサンプルコードでは以下のような結果が得られます。
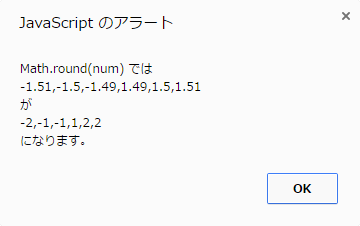
-1.5と1.5に注目するとわかりやすいと思います。勘違いしやすいところは与えられた引数のが負の場合、「絶対値について四捨五入を行い、負号をつける」のではない、と言うことです。以下のような丸めではないので注意しましょう。
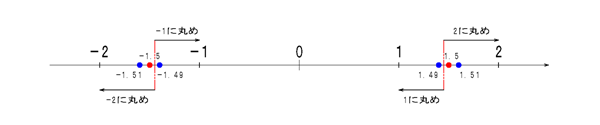
execelのワークシート関数roundがこのパターンなので電算処理一般がこのパターンだと思ってる人がいるかもしれませんがそんなことは全くありません。
MDNのMath.round()の説明には
number の小数部分が、.5 以上(.5 を含む)の場合、その引数は、次に大きい整数に切り上げられます。 number の小数部分が、.5 未満(.5 を含まない)の場合、その引数は、次に小さい整数に切り下げられます。
と書いてますが、「小数部分が、.5 以上(.5 を含む)の場合~」という表現が負の数に対してはちょっと正しくない言い回しなのかなーと思います。
このような挙動を示すので、端数が0.5ちょうどの時絶対値が同じでも「正の値を丸めて引く」のと「負の値を丸めて足す」のでは結果が異なるので注意したいところです。
ceil()メソッド
Math.ceil(num)は「引数として与えられた数値以上の最も小さい整数を返す」メソッドです。もしくは「常に+∞の方向へ丸める」と考えてもいいでしょう。
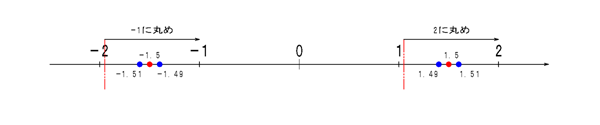
冒頭のサンプルコードでは以下のような結果が得られます。
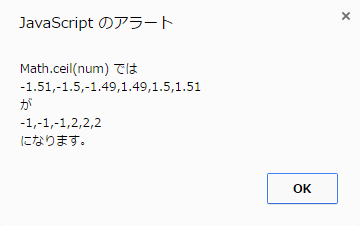
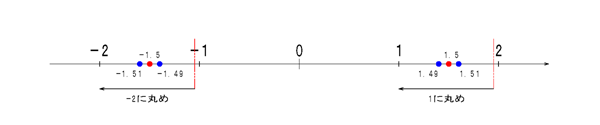
これは引数が正の場合でも負の場合でも同様です。正の場合に+∞、負の場合に-無限大に丸める(あるいは正負問わず常に0から遠ざける丸め)という仕様ではないです。
floor()メソッド
Math.floor(num)は「引数として与えられた数値以下の最も大きい整数を返す」メソッドです。「常に-∞の方向へ丸める」と言い換えることも出来ます。
冒頭のサンプルコードでは以下のような結果が得られます。
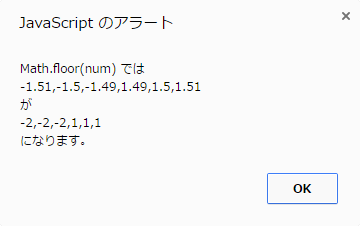
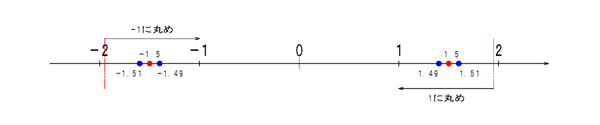
ceil()同様、引数が正の場合でも負の場合でも同じ処理を行います。正負いずれの場合でも常に0に向かっての丸めではありません。
trunc()メソッド
これは仕様が策定されてから、もしくは実装されてから日が浅いのでしょうか、MDNでも今のところ日本語訳の解説がありません。だれか翻訳お願いします。
Math.trunc(num)は「引数として与えられた数値とゼロ間の引数に最も近い整数を返す」メソッドです。常にゼロに近づける丸めです。「切り捨て」とはこういうものだ、と何となく思ってる人も少なからずいるかもしれません(実際には「負の実数に対する切り捨て」なるものは存在しません)。
冒頭のサンプルコードでは以下のような結果が得られます。
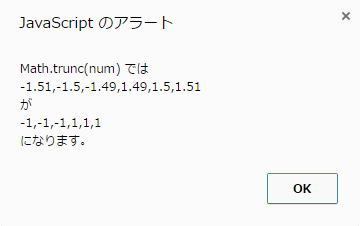
parseInt()オブジェクト
parseInt()オブジェクトは第一引数に与えられた「文字列」が表す数値を整数化して返すオブジェクトです。第二引数に基数を指定するのですが省略すると普通に10進数として返します。2を指定すると2進数として返します。十進算術ばかり扱う場合は第二引数のことはさしあたって忘れておいてもいいと思います。
で、この整数化なのですが、Math.trunc(num)と同じパターンです。

そしてこれは余談ですが、第一引数は文字列を渡すのですが、間違って数値オブジェクトを渡してもエラーを吐かずそれらしく変換結果を返します。いやらしいですね。
冒頭のサンプルコードでは以下のような結果が得られます。
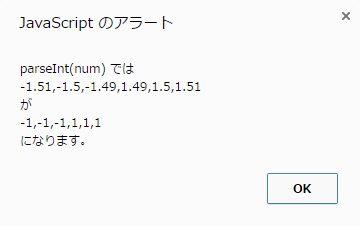
数値オブジェクトの文字列化メソッド
数値オブジェクトの文字列化メソッドにはnum.toFixed()、num.toPrecision()、num.toExponential(0)があります。これらはいずれも文字列を返すメソッドですが、表示上は数値の丸めを行ったがごとく振る舞います。丸めのパターンは

「引数として与えられた数値に最も近い整数を返す」のはMath.round(num)と同じなのですが最も近い整数が2つある、つまり小数点以下の端数が0.5ちょうどだった場合には正の値の場合は+∞側の整数を、負の値の場合は-∞側の整数を返す、というMath.raund(num)では間違とされる方のパターンです。ええぃ、ややこしい!
この辺り何が問題かと言うと表示は文字列化メソッドで、内部的な計算はMath.round(num)で…で中途の表示→計算続き→中途の表示→計算の続き…みたいな処理が必要になると中身と表示が違う、といったことが起こる懸念があったりします。
冒頭のサンプルコードではそれぞれ以下のような結果が得られます。
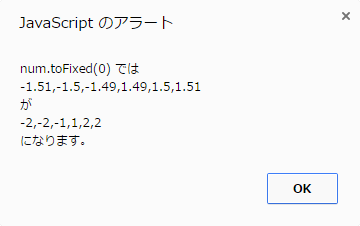
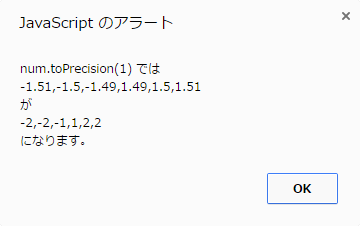
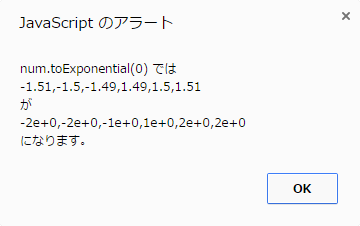
toExponential()は浮動小数点表示ですね。繰り返しになりますがこれらが返す値はあくまで文字列です。あとtoPresision()だけは引数に有効桁が指定できるので返り値は必ずしも整数(を現す文字列)ではありません。これはゼロ埋めもしてくれるので表示上は便利だったりもします。
JavaScriptの数値型とか
ここまで少数を整数に丸めるような話をしてきましたが、JavaScriptの変数の型には整数型とか実数型とか、浮動小数点の単精度とか倍精度とかの区別は有りません。全部ひっくるめて「数値型」です。なので、例えばMathオブジェクトの一連の丸めメソッドの返り値は「値の中身が整数に等しい」のであって、実数と同様、符号1ビット、仮数部52ビット、指数部11ビットの倍精度浮動小数で現されます。
より厳密には32ビット符号なし整数、32ビッ符号あり整数というのはあるんですが、少なくとも型として明示的に変換を行うような演算子は有りません。
四捨五入・切り捨て・切り上げ
解説の途中でもチラッと触れましたが、四捨五入・切り捨て・切り上げというのは算数教育で便宜的に用いられる「日本語表現」であって、数学的な定義を有するものではありません。かつその適用範囲は正の実数に限られます。つまり負の値の丸めの処理については都度定義が必要だということです。
高等学校以上の入学試験で負の値に対して四捨五入云々とかいう問題を出す学校はヤバいと思った方が良いです。
EXCELerの人はround・roundup・rounddownワークシート関数(そして書式表示上の桁上げ桁下げ)に馴染んでいて「数値の絶対値に四捨五入・切り捨て・切り上げを行って再度符号を与える」ような処理が一般的なことと思ってる方も少なからずいると思いますので、少なくともJavaScriptにおいてはそうではないということをご承知いただければ。
なおJIS Z 8401「数値の丸め方」では、その対象は正の値のみに限ることが明記されています。また負の値を対象とする場合はその絶対値に適用しなければならない、とも書いてあります。
まとめ
これらの丸めの方向を表にまとめてみました。
| 値の符号 | – | + | 戻り値の型 | ||||
|---|---|---|---|---|---|---|---|
| 少数点以下 | >0.5 | =0.5 | <0.5 | <0.5 | =0.5 | >0.5 | |
| Math.round(num) | -∞ | +∞ | +∞ | -∞ | +∞ | +∞ | 数値 |
| Math.ceil(num) | +∞ | ||||||
| Math.floor(num) | -∞ | ||||||
| Math.trunc(num) | 0 | ||||||
| parseInt(num) | |||||||
| num.toFixed(0) | -∞ | -∞ | +∞ | -∞ | +∞ | +∞ | 文字列 |
| num.toPrecision(1) | |||||||
| num.toExponential(0) | |||||||
最初からこれ書けばそれで用が足りた気がしないでもないですが、解説を自分で咀嚼して読んだりサンプル弄ってみるのもけっこう大事なことだと思いますこういうの覚えるうえでは。
というようなことを踏まえたうえで、JIS Z 8401 規則Aの丸め、いわゆる「最近接偶数丸め」とか「銀行丸め」とか言われるものの処理の仕方も考えたいと思いますがそれはまた今度。んじゃまた。

コメント