イラレでクリエイトユアタンブラーを自由にデザインしよう！

2012.06.06
Design

アドビイラストレーターは大の苦手のゴロドクです、どうも。

スターバックスコーヒーの｢クリエイトユアタンブラー｣（以下クリタン）って皆さんご存知ですか？繰り返し使えるコーヒー容器（タンブラー）なんですが、外周に台紙を差し込めるようになっていて自由にデザインできるんですよね。

今回はこの台紙形状のイラレデータを作ってみましたので、写真データなどを利用して超簡単にクリタンのデザインをする方法を紹介してみたいと思います。

きっかけは麗さんのブログから

そもそも何でそんなことをやろうかと思ったのかと言うと、先日麗（@X_urara_X）さんがブログでこんな記事を書いておりまして。

WEB屋 麗[Uruwashi] » Blog Archive » クリエイトユアタンブラー（Starbucks）を買ったので作ってみた。

こちらの記事を読んだ前後に麗さんとツイでゴニョゴニョおしゃべりしてたんですが

…というフリをいただいたので挑戦してみた次第。できるかどうかわからないけど見切り発車してみました。

とりあえずスタバの公式データをジロジロ眺めてみる

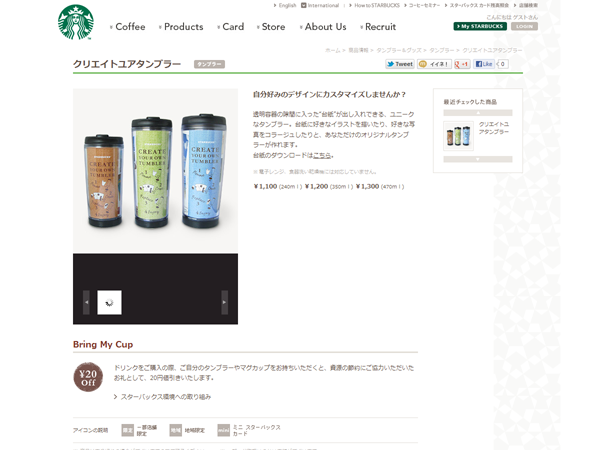
とりあえず手元に何のヒントもない状態だったのですが、スターバックスコーヒーの公式サイトで台紙を印刷して使うためのPDFデータがダウンロードできるらしいのでまずそちらを参考にしました。

クリエイトユアタンブラー | スターバックス コーヒー

上記のページでクリタン製品の概要とpdf台紙ダウンロードができますのでクリタンをご存じない方はとりあえずこれを読んでいただけるとどんなものかわかるかと思います。

製品はshort(240ｍｌ)、tall(350ｍｌ)、grande(470ｍｌ)の3種類のサイズがあり、いずれも飲み口より底が小さい円すい台（円すいの尖った先っちょ切った形）をひっくりかえした形状をしています。

実際にデザインするのはこの円錐台の外表面となりますので、これを平面に展開するとバームクーヘンを一部切り取ったような形になります。

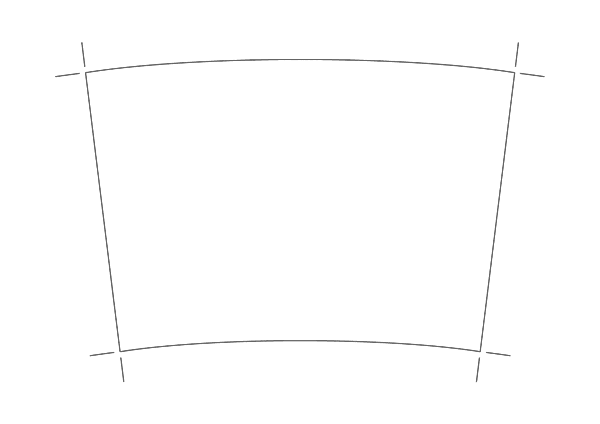
言葉で伝えにくいですが、要するに上の図のような「扇子の紙貼ってあるところの形」です。

で、とりあえず寸法的にどんなもんになってるのか、ダウンロードしたデータをイラレ経由でdxf（いわゆるCADの互換ファイル形式）に書き出し、いつも使ってるCAD（事情があって何を使ってるかは明かせません、悪しからず）で調べてみました。

私の使ってるCADでも要素の周長や2点間距離、面積や断面係数を測る（あるいは量る）機能がついており、いろいろ測ってみたんですが。

右上～左下、左上～右下の2対角を測ってみたら見事に寸法が違う。わずかではあるんですが、左右非対称で歪んでるんですね。左右の2直線の長さも異なっていました。

まぁ最後には印刷したものをカッターやハサミで切り取ることになるし、微々たる歪みなのでこだわるほどではないのかもしれないのですが、どうにもこういうのが私は気になっちゃう質でして。

左右対称になるようにデータを描きなおした

元データを参考に、左右対称になるようあらためてデータを描き直すことにして見ました。

元データどこが正確なのかは知るすべもないのですが、悩んでも埒があかないのでとりあえずこんな方針で描いて見ました。

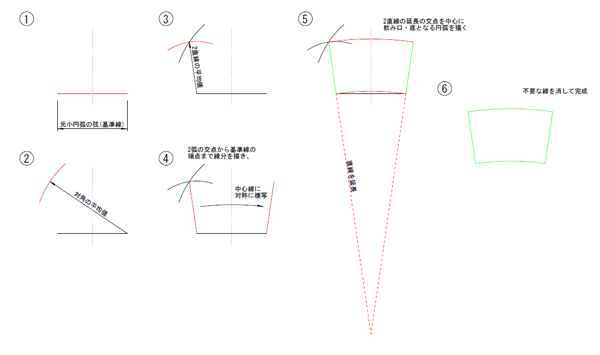
  1. 丸めたときに底になる部分の円弧（小さいほうの円弧）の2点間距離（弦長）は元データの通りとしこれを基準とする
  2. 対角長は元データの2点間距離の平均値を採用する
  3. 左右の直線長もそれぞれ2線分長の平均値を採用する
  4. 丸めたときに飲み口になる部分の円弧（大きいほうの円弧）は左右に直線の延長上にある交点を中心に描く単純円弧とする

図にするとこんな感じです。

これでゆがみのない左右対称な形状が出来ました。元データと重ねてもコンマ代の差しかないので十分実用レベルの形状になったと思います。

形状データの準備が出来たのでCADのほうからdxfで出力し、イラレで受け取ってパス化します。

イラレにイライラ

先ほどのdxfファイルをイラレで開いてみたらグループ化されてたのでまずこれを解除。

するとそれぞれ独立した2直線と2円弧のパスになるので、角端点を連結して1つの閉じたパスにする…のですが、これがよくわからなかった。

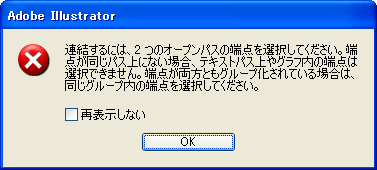
こんなメッセージが出てにっちもさっちも行かないので、麗さんにやり方を質問したところ

と言うような回答をいただきました。ありがとうございますー。

なんか私の作ったdxfデータに消し忘れの制御点が残っていて、パスのアンカーポイントだけ選択したつもりが余計な制御点まで含んで選択してたのが原因のようですね。

一応開いたパス同士の連結方法備忘録として残しておきますが、ダイレクト選択ツール（ツールパレットの白い矢印アイコン）で連結したい端点を2つ選択します。


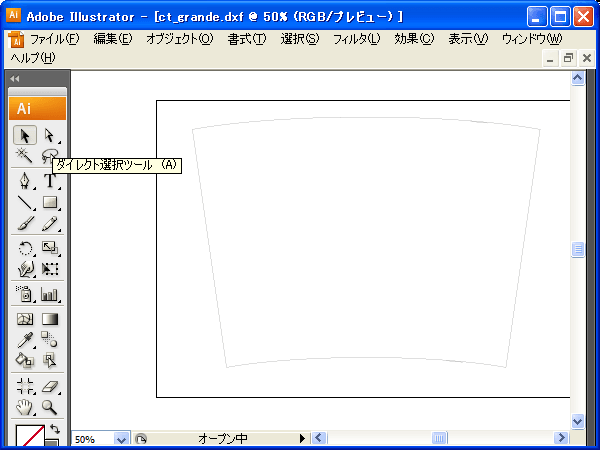
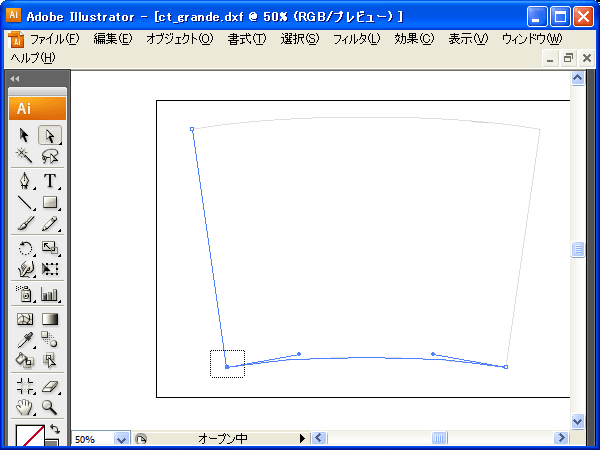
2点選択後メニューバーから【オブジェクト】-【パス】-【連結】を実行します。

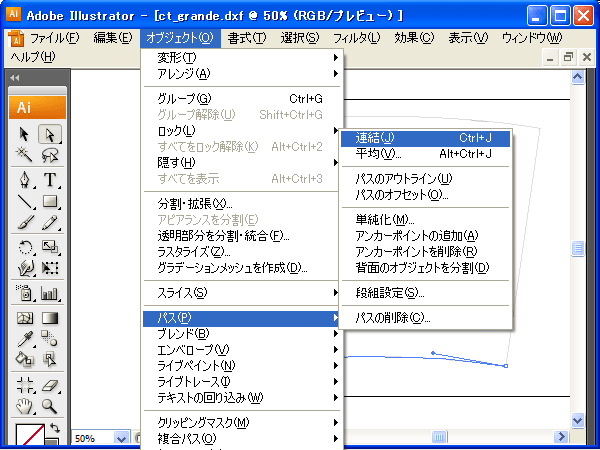
するとこんなダイアログが開いて、連結の方法を問われます。ここではスムーズ化する必要がないので「コーナー」を選択します。

おぉ、みごとパスの連結が出来ました。さらに同様の操作を3回繰り返し、扇型の4つ角全てを連結したら、1つの閉じたパスになる、と言うわけです。

素材は完成、あとはエンベローブで画像をはめ込むだけ！

そんな手順を踏んで出来上がったのがコチラのデータ。

ct_dat.zip（クリタン用形状データ）

short、tall、grandeそれぞれについてアドビアラストレーター（.ai）ファイル、cad互換（.dxf）ファイル、ついでにアナログ派の方向けにアクロバット（.pdf）も用意しました。

全部まとめて9ファイル、zip圧縮しております。上のリンクからダウンロードして適当な場所に解凍してください。

データの取り扱いですがダウンロード・個人利用はご自由にどうぞ。（いないと思うけど）商用と無断転載は勘弁してくださいな。

さてここからがダウンロードしたaiファイルの使い方です。え、今までの解説なんだったのって？知らんなりに苦労したから一応その辺を露出しておきたかったんですよｗ！

1.イラレでデータを開く

何はともあれまずはダウンロードして解凍したaiファイルをイラレで開きます。扇型の閉じたパスとトンボっぽいもの（切り離し時の補助線）が表示されると思います。

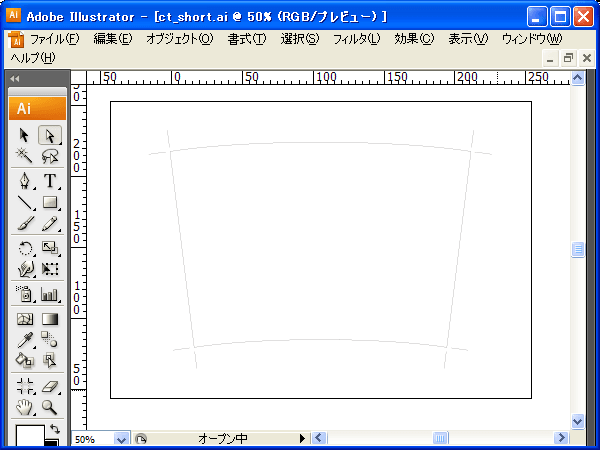
2.使いたい画像を配置する

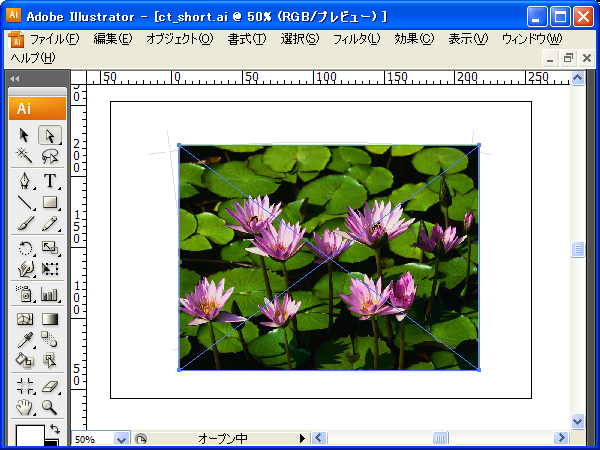
メニューバーの【ファイル】-【配置】から、クリタンに使いたい画像を配置します。

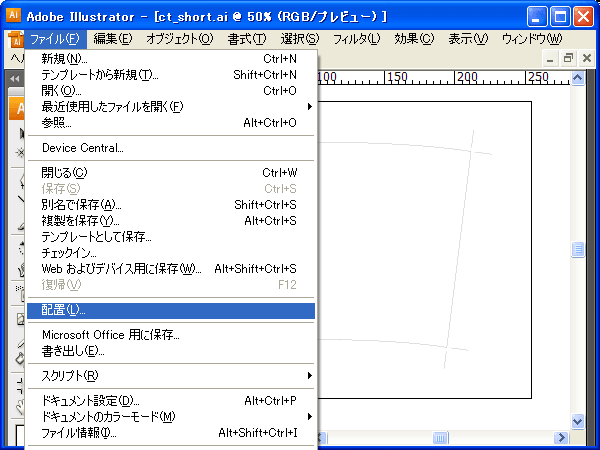
ここでは例としてWinXPにサンプルピクチャーとして入っている「Water lilies.jpg」を配置してみました。

3.画像を埋め込む

この画像をエンベローブ機能で扇型に変形したいんですが、そのままでは変形できないのでこのオブジェクトをドキュメントに埋め込みます。

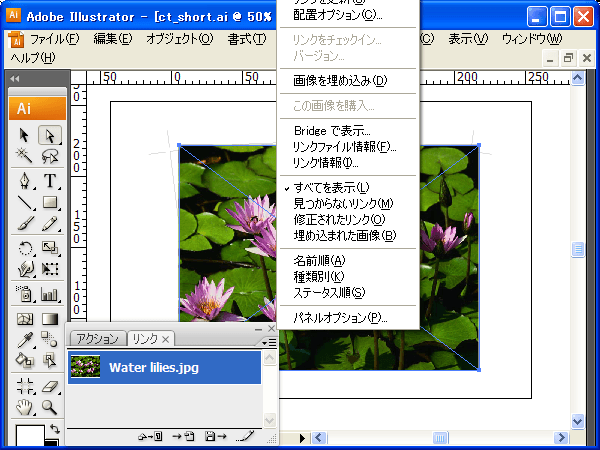
リンクウィンドウ（画面に表示されてないときは【ウィンドウ】-【リンク】を選択して表示）のメニューで先ほど配置した画像が選択状態（背景が青バックに反転）なのを確認します。

選択されていればリンクウィンドウ右上の▽ボタンを押してメニューを開き、その中の「画像を埋め込み」を選択します。

4.扇型のパスを最前面に移動

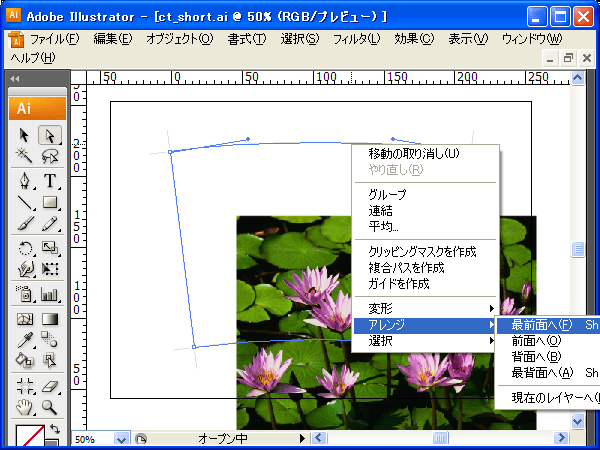
扇型の閉じたパスを選択し、コンテキストメニュー（Winなら右クリック）の【アレンジ】-【最前面へ】を選択します。

5.エンベローブで変形

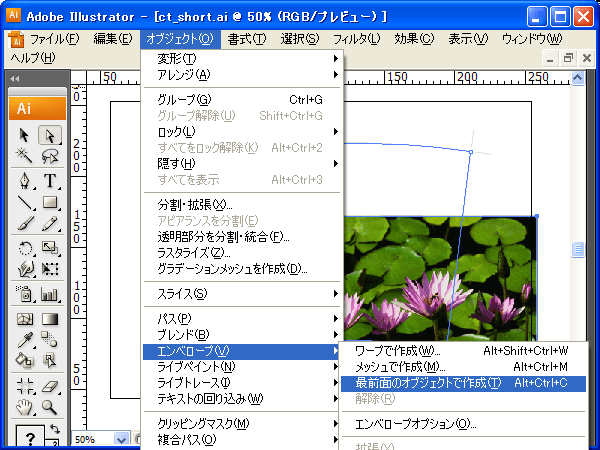
扇型の閉じたパスと、変形したい画像を両方選択します。この状態でメニューバーの【オブジェクト】-【エンベローブ】-【最前面のオブジェクトで作成】を実行します。

すると…なんということでしょう！先ほどまで四角かった画像が心の柔らかさを表すようなみごとな曲線、優雅な扇型になったではありませんか！…あ、今んとこは「ビフォーアフター」のナレーション風に脳内再生してくだしあ。

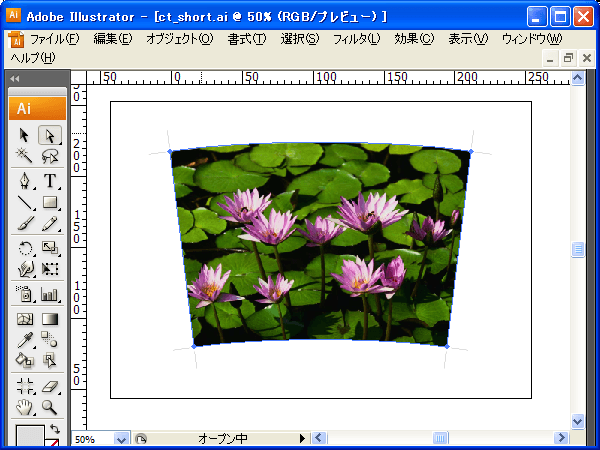
これで印刷用データの完成です。忘れずに別名で保存して印刷したらハサミやカッターナイフで綺麗に切り取り、クリタンに装着してやってください。

ちなみにaiファイルのアートボードサイズはshort、tall、grandeともA4横サイズですのでご家庭のプリンターで問題なく印刷できるかと思います。

こんな感じでイラレを使えば手持ちの写真から世界で一つだけのクリタンが超簡単に出来ちゃいますので、皆さんもデータダウンロードしてチャレンジしてみてくださいね。

閑話休題

えっと、エンベローブとか面倒なことしないでも画像の上にパス重ねて中だけ抜きゃあいいじゃん…というご意見もあろうかと思いますが、円すいや円すい台の表面に、中心軸に直角な同心の水平線をかくと、それを展開したときには弧になってしまいます（その辺は飲み口や底の円の展開を見れば容易に想像がつくかと思います）。

逆を言うと、展開図上に引いた直線は円すい状に丸めると直線（あるいは水平線）ではなくなるんですね…といったことは麗さんのブログ記事のほうでも触れられていましたね。

よってエンベローブで四角い画像を扇型にフィットしてやると丸めたときに綺麗に見えるようになる、と言うことなのです。

余談ついでに数学的な円すい台の性質を書いておくと

  • 大径：D1mm
  • 小径：D2mm
  • 高さ：Hmm

の円すい台は斜辺長Lが

となります。これを元に展開すると、展開後の図形は今まで見てきたとおり同心の二つの円の一部分切り取った形となります。この円の半径は、外側の円の半径をr1、内側の円の半径をr2とすると


となり、また切り取る弧の中心角θは

で、算術的に求めることが出来るのです。

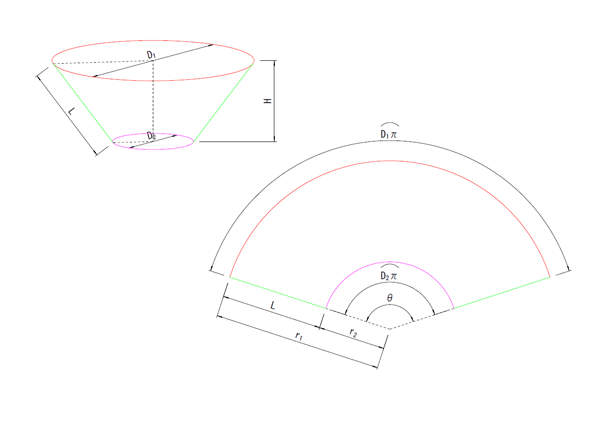
計算過程は割愛しますが、ピタゴラスの定理（直角三角形の直角を挟む辺a,bそれぞれ二乗したものの和は斜辺の二乗に等しい）と、円すいの軸直角な円の周長は展開後の弧長に等しいということを考えると比較的容易に上の式が導けますのでお暇な方はチャレンジしてみてください。

まとめ

難しいことは考えなくてもとりあえず今回作ったデータとイラレがあれば自由にクリタンデザインできるので、愛するハニーの写真でも大好きなアニメのキャラクターでも好きのもの作って自由に楽しんでください（でもキャラクターグッズとして売っちゃダメよ。あくまで個人が楽しむ範囲で）。

イラレは大の苦手でしたが今回麗さんに色々教えてもらってなんとなくパス関係のさわりくらいはわかった気がします。CADからのデータのインポートが可能だと幾何学的なデザインの絡むものならこれからCAD+イラレでいけそうなので私も色々楽しんでみたいと思います。

ちなみに今回のサンプル以外の成果品ですが私のマイクリタンデザインとして

こんなの作っちゃいました。てへぺろ。

画像データはクオリティの高さに定評あるぱくたそに掲載されているものを使わせていただきました。

あれ、まてよ、よく考えたらその前にオレクリタン持ってねいや。ウチも奥様プレゼントしてくれないかしら…

コメント

タイトルとURLをコピーしました