ネットでちょっと調べものしてたら大阪大学 竹村研究室ってとこのある論文(解説文書?)に人間の視野角について解説が載ってたので備忘録的に一部引用しておきます。デザイン関係の人は既知かも。
【2012年04月23日追記】関連記事「自分の眼の網膜解像度を測定できるアプリがちょっと新鮮で感動した」を書きました。
【2012年12月19日追記】関連記事書きました。
もうちょっとデザインに直接関わるお話です。
人間の視野角に関する諸数値
以下の通り数値的なところを抜粋しておきます。
- 人間の視野角は水平約200度,垂直約125度(下75度,上50度)
- 情報受容能力に優れる有効視野は水平30度,垂直20度程度
- 注視点が迅速に安定して見える安定注視野は水平に60~90度,垂直に45度~70度程度
- 映像に誘発される自己運動感覚(ベクション)は,臨場感の重要な指標であるが,その誘発は画角が水平20度程度から起こりはじめ,110度程度で飽和する
- 人の目の最小分解能は視力2.0の場合視角にして約0.5分(1/120度)
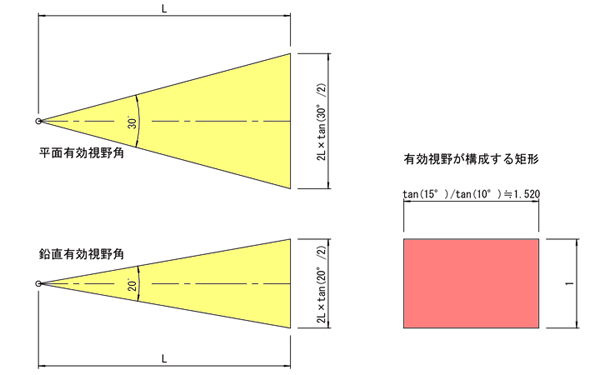
有効視野角がつくる矩形領域
ほほう、①をみると人間の目は水平方向に関しては180度を越えてるので一応真横よりちょっと後くらいまでは見えてるってことになります。しかしまともに脳内で認識できてるのは②の範囲くらいなので、視野角全体からするとかなり狭いってことですね。個人差はあると思いますが。この②の範囲を図化してみますと

こんな感じです。
ではこれを我々のよく使う比率の矩形と比べるとどうなるでしょう。下の図の上段に描かれてる破線の矩形は全て同じ有効視野角による矩形です。下段は左から順に4:3矩形(アナログテレビやVGA系列の解像度の比率)、√2:1矩形(JIS A版 紙サイズ比率)、黄金長方形、16:9矩形(いわゆるワイドサイズのテレビとかHDの比率)です。どの矩形も高さが同じになるように1としています。

どうでしょう。有効視野角に近いのは黄金長方形ですかね?16:9矩形は有効視野角よりかなり横長な比率なのですね…もっと人間の感覚に近い比率なのかと思ってましたが。私としては意外な結果です。
視線を動かさずにまともに認識できる領域がわかってると、一瞬で人間の脳に情報を伝えるレイアウトを考えるときに役に立つ…かもしれませんね。
解像度を計算してみる
話は変わって⑤を元に解像度関係の試算なんていうのもやってみましょう。視点から対象までの距離をL(cm)とすると、その時の対象上の読み取り可能な寸法pは2×L×tan[1/(120×2)]°(cm)です。また1インチ=2.54センチメートルなので解像度は2.54÷p(dot/inch)となります。Lを10cm~100cmまで10cm刻みに計算した結果は以下のようになります。
| 視点と対象の距離L(cm) | 1ピクセル寸法p(cm) | 解像度(pixel/inch) |
|---|---|---|
| 10 | 0.0015 | 1746 |
| 20 | 0.0029 | 873 |
| 30 | 0.0044 | 582 |
| 40 | 0.0058 | 437 |
| 50 | 0.0073 | 349 |
| 60 | 0.0087 | 291 |
| 70 | 0.0102 | 249 |
| 80 | 0.0116 | 218 |
| 90 | 0.0131 | 194 |
| 100 | 0.0145 | 175 |
なるほどなるほど。一般的に印刷物は350dpi以上って話がありますが、目から50cmくらいの距離で印刷物を読む(あるいは見る)と考えると視力2.0の人でもジャギーが判読できない、という妥当な数字なんですね、すごく納得です。近くで見ない看板なんかも解像度低くても大丈夫ってのが同じ計算で妥当なところを簡単に導き出せそうです。
とりあえず今のところ自分の理解できる範囲でこんな感じですけど、③・④については今のところわからないです。これらについても調べてみて役に立つことが何かわかったら新しいエントリ書くことにしますょ。

コメント